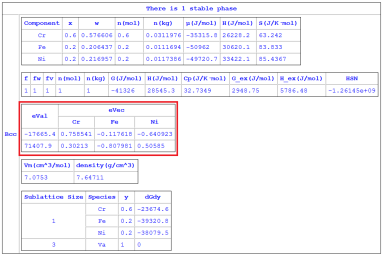
Hessian Matrix of Gibbs Energy
Pandat can calculate the determinant of Hessian matrix of Gibbs energy of a phase and the eigenvalues and eigenvectors of the Hessian matrix.
Since there is one dependent molar fraction for the molar fraction variables (x1,x2,⋯,xn), one of the components is selected as the dependent one. Without loss of generality, xn is selected as the one, i.e., the last component is considered as the solvent. Then, the second derivatives of Gibbs free energy of a phase form the Hessian matrix, which is an (n-1)×(n-1) symmetrical matrix.
Its determinant is given by
The determinant of Hessian matrix for phase f is available from “HSN(@f)”. The value of “HSN(@f)” is independent of the selection of the solvent component[2021Mor, 2022Che].
The above Hessian matrix has (n-1) eigenvalues and each eigenvalue has a corresponding eigenvector. In general, both eigenvectors and eigenvalues depend on the choice of the solvent component. These eigenvalues can be used to identify the spinodal boundaries. At the spinodal boundary, one of the eigenvalues will be zero for every choice of the solvent element. The eigenvalues and their eigenvectors are available from “eVal(#*@f)” and “eVec(*#*@f)”, respectively. The individual eigenvalues can be accessed in the Table as “eVal(#1@f)”, “eVal(#2@f)”, … ,“eVal(#n-1@f)”. The eigenvalues are inherently sorted in the ascending order. Thus, “eVal(#1@f)” is the minimum eigenvalue and “eVal(#n-1@f)” is the maximum eigenvalue. Each eigenvalue has an eigenvector. For example, eVal(#1@f) has an eigenvector of (eVec(C1#1@f), eVec(C2#1@f),…, eVec(Cn-1#1@f)), where Ck is the name of the kth component. The keywords HSN, eVal and eVec are listed in Table 1 in Section Pandat Table Format Syntax.
The “solvent” component can be defined while using “Thermodynamic Property” calculation, or defined in Pandat Batch file (.pbfx). For instance, “<solvent name="Fe" />” can be added to the batch file for choosing “Fe” as the solvent element. If “solvent” component is not defined, Pandat will use a special treatment (called orthogonalization [2022Kon] ) that ensures both the eigenvalues and the eigenvectors are independent of the solvent component. This special treatment would be very helpful in analyzing spinodal decomposition in high-entropy alloys. Note that eigenvalues are generally not calculated during thermodynamic calculation for efficiency. But it can be calculated by adding the flag “<Hessian value="true" />” to the batch file. Sample batch files for calculating eigenvalues/eigenvectors by choosing a solvent (Eigenvalues_solvent_Fe.pbfx) or without choosing a solvent element (Eigenvalues_nosolvent.pbfx) can be found in the Examples folder (\Pandat 2025 Examples\PanPhaseDiagram\Eigenvalues).
Figure 1: Calculated eigenvalues/eigenvectors without choosing the solvent component in Fe-Cr-Ni ternary alloy (from the batch file “Eigenvalues_nosolvent.pbfx”).
Figure 2: Calculated eigenvalues/eigenvectors by choosing “Fe” as the solvent element in Fe-Cr-Ni ternary alloy (from the batch file “Eigenvalues_solvent_Fe.pbfx”)
Calculation of Spinodal Curve Using the Eigenvalue of Hessian Matrix
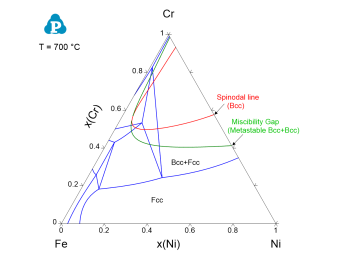
One of the important application using the eigenvalues of Hessian matrix is to calculate the spinodal line of a spinodal decomposition phase. The eVal(@*) can be added as an condition in the batch file to find the spinodal line as contour line. Below is the example to calculate the spinodal line of the Bcc phase, and the calculated spinodal line is superimposed on the Fe-Ni-Cr isothermal section as shown in Figure 3.
<condition>
<contour name="Spinodal" property="eVal(#1@Bcc)" start="0" stop="10" step="100" />
<equilibrium_type type="individual" />
<scanline_density value="1" />
<Hessian value="true" />
</condition>
Figure 3: Calculated Fe-Cr-Ni isothermal section at 700 °C together with the metastable miscibility and spinodal lines (from the batch file “Spinodal_boundary_on_section.pbfx”)
[2021Mor] J.E. Morral, S. Chen, Stability of High Entropy Alloys to Spinodal Decomposition, J. Phase Equilib. Diffus., 42 (2021) 673–695
[2022Che] S. Chen, R. Schmid-Fetzer, J.E. Morral, Calculation of Critical Points, J. Phase Equilib. Diffus., 43 (2022) 968-978.
[2022Kon] S.R. Koneru, K. Kadirvel, Y. Wang, High-Throughput Design of Multi-Principal Element Alloys with Spinodal Decomposition Assisted Microstructures, J. Phase Equilib. Diffus., 43 (2022) 753-763.